Élection du responsable du projet Debian 2012

Calendrier

Période de candidature dimanche 4 mars 2012 00:00:00 UTC samedi 10 mars 2012 23:59:59 UTC
Période de campagne dimanche 11 mars 2012 00:00:00 UTC samedi 31 mars 2012 23:59:59 UTC
Période de scrutin dimanche 1er avril 2012 00:00:00 UTC samedi 14 avril 2012 23:59:59 UTC

Veuillez noter que le nouveau mandat du responsable du projet débutera le 17 avril 2012.

Nominations

  1. Wouter Verhelst [[email protected]] [message de candidature] [programme]
  2. Gergely Nagy [[email protected]] [message de candidature] [programme]
  3. Stefano Zacchiroli [[email protected]] [message de candidature] [programme]

Données et statistiques

Cette année, comme d'habitude, des statistiques sur les bulletins et les accusés de réception seront rassemblées périodiquement durant la période du scrutin. De plus, la liste des votants sera enregistrée. La feuille d'émargement sera également disponible. Veuillez noter que l'élection du responsable du projet se fait à bulletins secrets, la feuille d'émargement sera produite avec un condensé de l'alias des votants au lieu de leur nom ; l'alias sera envoyé aux votants avec l'accusé de réception de leur bulletin pour qu'ils puissent vérifier que leur vote a correctement été pris en compte. Pendant le scrutin, la feuille d'émargement sera factice ; après la clôture du scrutin, la feuille finale sera mise en place. Veuillez noter que pour les votes à bulletin secret le résumé MD5 sur la feuille d'émargement est généré aléatoirement, sinon elle pourrait révéler des informations confidentielles sur le votant.

Quorum

Avec la liste actuelle des développeurs votants, nous avons : 

 Nombre actuel de développeurs              = 948
 Q ( racine carrée(nb de développeur) / 2 ) = 15,3948043183407
 K min(5, Q )                               = 5
 Quorum  (3 x Q )                           = 46,184412955022

Quorum

Majorités requises

Tous les candidats ont besoin d'une majorité simple pour être élus.

Majorité

Résultat

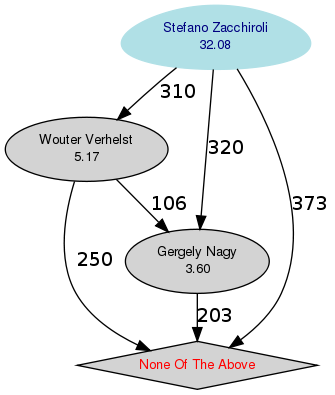
Affichage graphique des résultats

Dans le graphique ci-dessus, les nœuds en rose n'ont pas obtenu la majorité requise, le bleu est le gagnant. L'octogone est utilisé pour les options qui n'ont pas battu l'option par défaut.

Dans le tableau suivant, la correspondance ligne[x] colonne[y] représente le nombre de suffrages où le candidat x est classé devant le candidat y. Une explication plus détaillée de la matrice des gagnants peut vous aider à comprendre ce tableau. Pour comprendre la méthode Condorcet, l'entrée de Wikipedia est assez instructive.

Grille des résultats
 Option
  1 2 3 4
Option 1   203 37 310
Option 2 97   34 281
Option 3 347 354   385
Option 4 60 78 12  

En regardant à la ligne 2, colonne 1, Gergely Nagy est classé devant Wouter Verhelst sur 97 bulletins.

En regardant à la ligne 1, colonne 2, Wouter Verhelst est classé devant Gergely Nagy sur 203 bulletins.

Couples de défaites

Contenu de l'ensemble de Schwartz

Gagnant

Debian utilise la méthode Condorcet pour les élections. De façon très simpliste, la méthode Condorcet pure pourrait s'expliquer ainsi :
Considérer tous les couples possibles de candidats. Le gagnant selon Condorcet, s'il existe, est le candidat qui bat chacun des autres candidats en duel singulier. Le problème est que dans des élections complexes, il pourrait y avoir des relations circulaires dans lesquels A bat B, B bat C et C bat A. La plupart des variations de la méthode Condorcet utilisent divers moyens pour résoudre ces cas. Veuillez lire la méthode Schulze pour de plus amples informations. La variante de Debian est expliquée dans la constitution, au paragraphe A.6.

Secrétaire du Projet Debian